Raytracingsimulation eines Schwarzen Loches

Newtonsche Simulation

Einsteinsche Simulation

Die beiden Bilder zeigen eine komplexe Szenerie, die ein Gefühl für die Raumkrümmung vermitteln soll, die nach der Einsteinschen Gravitationstheorie durch Masse verursacht wird. Die "Newtonsche Simulation" zeigt eine weite Meeresfläche, über der eine kugelförmige Masse mit einer fußballähnlichen Oberflächenstruktur schwebt. Durch deren gravitative Anziehungskraft wird das Wasser etwas emporgehoben, die Kugelmasse befindet sich also genau über dem Wasserberg. Schräg nach hinten durchstößt diesen eine weiße Stange, mit der der räumliche Zusammenhang zu den dahinterliegenden Objekten etwas verdeutlicht werden soll. Das hintere Stangenende trifft sodann auf einen rot leuchtenden Ikosaeder, der auch die Kugelmasse von hinten anleuchtet; ganz schwach ist der Lichtschein auf der rechten Seite zu erkennen. Die dahinterliegende, umgekippte rotschwarz gesprenkelte Säule befindet sich in etwa auf der Höhe des aus Ziegeln aufgebauten Turms mit den beiden abgeplatteten Goldkugeln. Die einzelnen Effekte, die die Raumkrümmung bei der Betrachtung dieser Szenerie verursacht, werden im folgenden beschrieben.

Die farbe Kugel im linken Teil der "newtonschen Simulation" musste aus Gruenden der Uebersichtlichkeit in der "einsteinschen Simulation" leider weggelassen werden.

Der Gravitationslinseneffekt

Das Grundprinzip der Allgemeinen Relativitätstheorie ist, daß Masse den Raum krümmt und somit auch Lichtstrahlen einen anderen Weg nehmen als dies im flachen (euklidischen) Raum der Fall wäre. Ähnlich wie ein schnell bewegtes Teilchen, das durch einen massiven Körper abgelenkt wird, bewegen sich auch Lichtstrahlen "um eine Masse herum".

Der einfachste Fall ist die Schwarzschildlösung, die das Vakuumfeld einer kugelsymmetrischen, nichtrotierenden und elektrisch ungeladenen Massenverteilung beschreibt. Eine Besonderheit dieser Lösung ist das Auftreten eines Ereignishorizontes, falls die verursachende Masse innerhalb des Schwarzschildradius

lokalisiert ist. Als Ereignishorizont wird der Rand eines Gebietes bezeichnet, das nur in einer Richtung von Materie oder Licht durchquert werden kann - alles kann hinein, aber nichts mehr hinaus. Kein Ereignis, daß im Inneren des Ereignishorizontes stattfindet, kann sich nach außen hin jemals bemerkbar machen - die Innenregion ist daher "kausal entkoppelt". Bei realen Objekten wie Sternen oder Planeten treten derartige Phänomene nicht auf, da deren Massen weit über den Ereignishorizont hinausreichen - die Sonne etwa müßte auf 2.5km schrumpfen, die Erde gar auf 0.8cm, damit ein Ereignishorizont entstehen könnte. Dennoch kann man jeder beliebigen sphärisch symmetrischen Masse einen Schwarzschildradius gemäß obiger Formel zuordnen und somit die Masse in Einheiten einer Länge ausdrücken. Bei der hier vorgestellten Simulation wird eine Kugelmasse mit dem Schwarzschildradius 0.5 Meter verwendet, die aus einem Abstand von 25 Metern beobachtet wird.

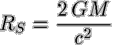
Ein Lichtstrahl wird durch eine Masse mit dem Schwarzschildradius 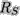um den Winkel

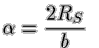
abgelenkt, wobei b den minimalen Strahlabstand zur ablenkenden Masse bezeichnet:

Eine Masse, deren Wirkung groß genug ist, um Licht abzulenken, wird daher auch als Gravitationslinse bezeichnet. Die Lichtablenkung einer Gravitationslinse ist umso stärker, je näher ein Lichtstrahl an der Linse vorbeiläuft:

Dieses Verhalten ist vollkommen anders, als es bei gewöhnlichen Sammellinsen aus Glas der Fall ist; dort wird das Licht umso stärker abgelenkt, je weiter es von der optischen Achse entfernt ist:

Auch eine Zerstreungslinse entspricht nicht dem Verhalten einer Gravitationslinse, denn die Strahlen werden ja auch im Gravitationsfeld in einer gewissen Weise gebündelt. Offensichtlich haben Gravitationslinsen ein völlig anderes, grundsätzlich verschiedenes Abbildungsverhalten als gewöhnliche optische Linsen; dieses zu veranschaulichen, ist das Ziel dieses Projektes.

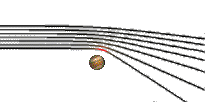
Eine ungewöhnliche Eigenschaft ist etwa, daß ein Gegenstand dem Beobachter mehr als einmal erscheinen kann, wie der leuchtende Ikosaeder oder der Ziegelzylinder mit seinen abgeplatteten Goldkugeln; dieses Verhalten ist auch unmittelbar einsichtig, denn Lichtstrahlen können auf zwei Wegen zum Beobachter gelangen:

Dabei ist der Weg des oberen Strahles kürzer als der unteren, der Gegenstand erscheint über den oberen Lichtweg näher und infolgedessen auch heller zu sein. Deutlich ist dies an der Abbildung des Ikosaeders zu erkennen, das rechte Bild ist etwas verzerrt "nach außen" gedrückt worden, dennoch aber ungefähr gleich hell wie das Original. Das Gegenbild hingegen befindet sich auf der anderen Seite der Gravitationslinse und ist bedeutend kleiner und lichtschwächer. Dazu kommt, daß das Gegenbild spiegelverkehrt ist, was durch den Tisch, auf dem der Ikosaeder steht, sehr deutlich zum Tragen kommt:

(invers, klein)

(aufrecht, verzerrt)

Es gibt somit einen bestimmten Winkel, eine Art "Inversionsradius", der eine Grenze zwischen spiegelverkehrten und normal, wenn auch verzerrt, abgebildeten Objekten darstellt. Außerhalb dieses Inversionsradius werden die Lichtstrahlen etwas nach außen gedrängt, sodaß die Abbildungen nach außen gebogen scheinen (vgl. Ziegelzylinder und Ikosaeder). Innerhalb des Inversionsradius treten alle außen sichtbaren Objekte nochmals auf - allerdings kleiner und spiegelverkehrt. Das Licht dieser Bilder wird nicht nur abgelenkt, sondern läuft zudem "um die Masse herum".

Liegt ein Objekt genau hinter der Gravitationslinse, dann treten nicht mehr zwei Bilder "innen" und "außen" auf, sondern beide Bilder verschmelzen zu einem Ring mit der Gravitationslinse im Zentrum. Diese Erscheinung ist auch als Einsteinring bekannt und in der Natur, zumindest annähernd, beobachtet worden. Der Beobachter befindet sich gleichsam im "Brennpunkt" der Linse, ein einziger Objektpunkt tritt als linienförmiges Bild auf und wird daher maximal vergrößert. In der Simulation befindet sich dieser Objektpunkt auf der schiefen schwarzroten Säule; auch zeigt sich, daß die gleichartigen Oberflächenstrukturen der Säule immer stärker verzerrt werden, je näher sie dem Inversionsradius kommen - bis sie sich schließlich ganz dessen runder Form anschmiegen und den Einsteinring bilden.

All diese Phänomene, die mit dem Einsteinring in Zusammenhang stehen, sind auch schon in der Natur beobachtet worden, allerdings in viel kleinerem Maße; während die Strahlen hier um einige Grad abgelenkt werden, ist bei den heutigen astronomischen Beobachtungen eine Größe von 15 Bogensekunden der Normalfall.

Ein interessanter Effekt, bei dem die räumliche Struktur der Szenerie besonders nett in Erscheinung tritt, fällt bei dem Holztisch auf, der als Ständer für die Ikosaeder-Lichtqueller dient: Während man in der newtonschen Simulation nur die Oberseite des Tisches sehen kann, ist durch die Raumkrümmung am linken Tischrand, wo die Krümmung am stärksten ist, auch ein Teil der Unterseite zu sehen. Das von der Tischunterseite stammende Licht wird durch die Wirkung der Masse nach oben hin ins Auge des Beobachters abgelenkt, die Tischplatte selbst scheint völlig verbogen zu sein, obwohl sie an Ort und Stelle nach wie vor genauso eben ist wie in der newtonschen Simulation.

Der Ereignishorizont

Der Ereignishorizont selbst kann nicht sichtbar sein, da keinerlei Licht von ihm nach außen gelangen kann. Dennoch kann man sich vorstellen, daß er mit einer dünnen Membran umgeben wird, von der Licht ausgesendet werden kann, sodaß das Licht von dort ein paar Eindrücke über die Raumkrümmung im noch zugänglichen Bereich kurz außerhalb des Horizontes vermitteln kann. In Wirklichkeit würde jedwedes Licht von dort extrem stark rotverschoben werden, sodaß die Oberflächenstruktur der Membran tiefrot bis infrarot (und damit unsichtbar) wäre. Die gravitative Rotverschiebung wurde daher bewußt nicht mit in die Simulation aufgenommen. Allerdings wird einfallendes Licht in genau demselben Ausmaß blauverschoben wie ausfallends rotverschoben wird. Wenn von außen einfallendes Licht auf einer (radial) unbewegten Fläche reflektiert wird, so erscheint sie in der gleichen Farbe wie im flachen Raum, insofern ist die vorgestellte Simulation physikalisch korrekt. Vorausgesetzt allerdings, das betrachtete Objekt reflektiert alle Wellenlängen gleichzeitig, andernfalls treten doch wieder Farbverschiebungen auf. Im Extremfall fällt sichtbares (weißes) Licht als Röntgen- oder gar Gammastrahlung auf das Objekt ein, das so in diesem Wellenlängenbereich transparent wird. Obwohl also etwaige reflektierte Lichtstrahlen für einen außenstehenden Beobachter als weißes, sichtbares Licht zurückkämen, wird das Objekt unsichtbar, wenn es nur nahe genug dem Schwarzschildhorizont kommt!

Im Nahbereich des Ereignishorizontes treten nun Phänomene auf, die ganz und gar ungewöhnlich sind: Während in genügend großem Abstand die Bahn des vorbeiziehenden Lichtes noch durch Hyperbeln angenähert werden kann, ist diese Näherung bei kleinen Abständen unzulänglich bis falsch. Das Licht kann hier so stark abgelenkt werden, daß es zur Lichtquelle zurückkehrt oder, anders ausgedrückt, der Beobachter sich selbst sieht. Noch näher am Ereignishorizont gibt es schließlich eine Bereich, in dem das Licht mehrmals das Schwarze Loch umrunden oder sogar auf einer Kreisbahn hängen bleiben kann. Je näher der Blickwinkel des Beobachters diesem "Rotationsradius" kommt, desto öfter (und kleiner) wird die gesamte äußere Welt schalenförmig verzerrt abgebildet, zusätzlich zu den oben beschriebenen "großräumig" auftretenden Gravitationslinseneffekten.

Im Inneren des Rotationsradius schließlich werden alle Lichtstrahlen auf die "Oberfläche" des Schwarzen Loches (die willkürlich aufgestülpte Membran) geleitet. Äußere Strahlen spiralen langsam, nach mehreren Umläufen, hinein, Sichtstrahlen, die direkt auf das Zentrum des Schwarzen Loches zielen, treffen dieses nahezu unverfälscht. Die direkt vor dem Beobachter liegende Seite des Schwarzen Loches scheint völlig unverändert sichtbar zu sein, aber bald fällt auf, daß auch der "Nordpol" der Kugel sichtbar ist (der Südpol wäre ebenfalls sichtbar, ist jedoch nicht beleuchtet und liegt daher im Dunkeln). Das Licht (äquivalent der Sichstrahl des Beobachters) spiralt gleichsam von oben herab auf den Pol und darüber hinaus sogar auf die Rückseite. Nun ist auch der von hinten rot angeleuchtete Teil der Kugel zu sehen - nicht nur eine Seite des Schwarzen Loches ist sichtbar (wie man es vom Alltag gewohnt ist), sondern seine gesamte Oberfläche!
Allein das ist bereits ungewöhnlich, aber hinzu kommt, daß die gesamte Oberfläche nicht nur von einer Blickrichtung aus, sondern aus jeder beliebigen Richtung aus sichtbar ist!

Weiteres zum Thema Schwarze Löcher auf der Seite der `Black Earth' (1997)

Die Berechnungen wurden im März 1993 durchgeführt.

Werner Benger, Oktober 1994