The Black Earth

Wenn man die Eigenschaften der von Einstein vorhergesagten Raumkrümmung im Gravitationsfeld anschaulich erfassen möchte, ist recht zweckmäßig, ihre Effekte auf Objekte wirken zu lassen, die man aus dem Alltag kennt, sodaß man anhand der durch die Raumkrümmung hervorgerufenen Änderungen eine Vorstellung davon bekommt, was die Krümmung des Raumes wirklich bedeutet.

Die Erde selbst ist ein nicht ganz unbekanntes Objekt, und so soll hier gezeigt werden, was geschieht, wenn sich die Erde eines Tages plötzlich und unvermittelt in ein Schwarzes Loch verwandeln würde.

Dazu braucht man also erst einmal die Erde in einem `virtuellen Labor', am besten, gleich mit dem Mond dazu, damit das System nicht nur einfach aus einer Kugel besteht. In Wirklichkeit ist der Mond von der Erde ca. 60 Erdradien entfernt. Aber im virtuellen Labor kann man ja `Gott' spielen und den Mond in die interessantere Entfernung von 1.5 Erdradien setzen. Interessanter ist dieser Abstand deshalb, weil bei einem Schwarzen Loch in einem Abstand vom 1.5 des Schwarzschildradius der sog. Photon-Orbit liegt. Der Photon-Orbit ist derjenige Abstand, in dem Photonen, als Licht, um das Schwarze Loch auf einer Kreisbahn herumfliegen können; hierbei treten einige interessante Effekte auf, die im folgenden behandelt werden sollen. Um aber die Situation etwas realistischer werden zu lassen, sollte man den `Labortisch' besser weglassen. In Wirklichkeit ist ja das System Erde-Mond vom Sternenhimmel umgeben. Und so scheint hier der Mond über dem nächtlichen Zentralafrika vor den Sternenhintergrund des SAO Kataloges der 258.000 hellsten Sterne (zusammengestellt vom Smithsonian Astrophysical Observatory). Die Daten der Erdoberfläche (Tag- und Nachtsicht) stammen von Living Earth ®, die Mondoberfläche wurde mithilfe der Daten der US-Raumsonde Clementine gestaltet. Diese Szene ließe sich noch realistischer gestalten, wenn zur Erde ihre Atmosphäre hinzugefügt wird (hier um einen Faktor 15 größer dargestellt als in Wirklichkeit). Allerdings steigt dann der Rechenaufwand um das 60fache, weshalb in den folgenden Simulationen darauf verzichtet wird. Was nun geschähe, wenn die Erde soviel Masse hätte, daß sie 90% ihres Schwarzschildradius ausfüllen würde? Das ist ungefähr diejenige Größe, bei der ein Stern noch stabil bleiben kann, das genaue Limit liegt bei 9/8 des Schwarzschildradius, was einer Ausfüllrate von 88% entspricht. Wird ein Objekt in einen Raumbereich kleiner als dieses Limit zusammengedrückt, endet er unaufhaltsam im Gravitationskollaps, als Schwarzes Loch. Die Gravitationskraft eines derart kompakten Objektes ist so stark, daß Lichtstrahlen quasi `hinuntergezogen' werden. Ein Lichtstrahl, der also im flachen Raum über dem Nordpol gerade vorbeilaufen würde (siehe voriges Bild) wird also auf den Nordpol hin abgelenkt und man kann den Nordpol - und die Gebiet darüber hinaus - auch einer Beobachterposition über dem Äquator sehen. Gleiches geschieht mit dem Südpol, auch ihn sieht man, in einem Bild mit dem Nordpol. Analoges gilt aber auch für die Äquatorgegend: Das Licht läuft auch hier um die Erde herum und man kann Tag- und Nachtseite auf einmal sehen, und über die Nachtseite hinaus taucht wieder die Tagseite auf, weil man einmal `um die Erde herum' sieht, wie auch rechts der Tagseite wieder die Nachtseite sichtbar wird. Man kann also die gesamte Oberfläche eines Schwarzen Loches auf einmal (oder sogar öfter als einmal) sehen. Realistischerweise muß man aber dazu sagen, daß die hier vorgestellte Simulation eigentlich falsch ist. Wenn man von jedem Punkt aus die gesamte Oberfläche sehen kann, kann man auch von jedem Punkt der Oberfläche aus den gesamten Sternenhimmel sehen. Das heißt, daß über jedem Punkt der Oberfläche auch die Sonne zu sehen ist, da ihr Licht durch die Raumkrümmung auch auf die sonnenabgewandte Seite, die eigentliche Nachtseite, gelenkt wird. Der Unterschied zwischen Nacht und Tag verschwimmt somit, und es ist - eigentlich - überall gleich hell. Dieser Einfluß wurde in den hier vorgestellten Simulationen nicht nachempfunden, einerseits, weil dies simulationstechnisch relativ schwierig zu bewerkstelligen wäre, andererseits, weil durch diese Darstellung der Unterschied zwischen Vorder- und Hinterseite klarer ersichtlich und damit anschaulicher ist. Wie sieht das nun von der Erdoberfläche aus, für jemanden, der `mittendrin' im gekrümmten Raum ist, nicht nur in sicherer Entfernung weit außerhalb? Hier sieht man nun den Blick auf den Mond, im Abstand von 1.1 Erdradien. Die ungewohnte Perspektive ist auffällig: Der Mond erscheint zu einer Ellipse verzerrt, der Sternenhimmel erscheint auf den Horizont hin immer stärker zusammengequescht - wie erwähnt, kann man ja von jedem Punkt der Oberfläche aus den gesamten Sternenhimmel sehen, da das Sternenlicht spiralförmig von allen Seiten herabfällt. Aber auch die gesamte Erdoberfläche ist von jedem Punkt auf der Oberfläche sichtbar, da Licht, das nicht steil genug vom Erdboden aufsteigt, wieder auf die Erdoberfläche zurückgezogen wird. Daher erscheint am fernen Horizont unterhalb des Mondes wieder die Tagseite der Erde. 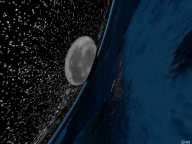Es spricht aber nun nicht wirklich etwas dagegen, die Masse der Erde soweit ansteigen zu lassen, daß die Erdoberfläche genau am Schwarzschildradius liegt (ein Vielfaches der Sonnenmasse, deren Schwarzschildradius ca. 2.5km entspricht. Bei einem Erdradius von etwas mehr als 6000km entspricht dies also einer Masse von ca. 2500 Sonnen, die auf das Volumen der Erde zusammengequetscht sind.) Ein derartiges Objekt ist zwar physikalisch nicht mehr stabil, aber simulieren kann man es nichtsdestoweniger trotzdem. Gar so unterschiedlich ist die Perspektive gegenüber der vorigen Variante nicht mehr, die Verkrümmung des Horizontes ist etwas stärker, wie auch die Verzerrung des Mondes und des Sternenhimmels. Man sollte sich jedoch vor Augen halten, daß dies einer der letzten Augenblicke (nicht der letzte, da der Abstand vom Erdmittelpunkt noch immer 10% außerhalb des Ereignishorizontes liegt) ist, den ein in das Schwarze Loch `Erde' fallender Raumfahrer sehen würde. Von hier kann er gerade noch mit einer entsprechend starken Rakete entkommen, aber etwas weiter, und aus der Region jenseits des Ereignishorizontes gäbe es kein Entkommen mehr. Der `letzte Blick' auf den Mond könnte so aussehen wie in diesem Bild: Hier ist ein fallender Astronaut nur noch 10km vom Ereignishorizont entfernt, auch ein auf der kollabierenden Erde zurückgebliebener Bergsteiger auf einem etwas aufgeschütteten Mt. Everest in der Sahara hätte denselben Ausblick (wenn man die durch die unterschiedliche Bewegung der beiden Beobachter hervorgerufenen speziell relativistischen Effekte außer acht läßt, d.h. der Astronaut nicht `frei' fällt, sondern sich noch gerade irgendwie hält). Doch nun wieder etwas zurück, nach außerhalb, in die interessanten Regionen des bereits zuvor erwähnten Photon-Orbit. Auf den ersten Blick scheint dieser Bereich nicht sonderlich auffällig, weder der Blick zum Mond selbst, noch in die Gegenrichtung. Zwar erscheint auch hier der Sternenhimmel am Horizont immer mehr verzerrt, und man kann auch am Erdrand erkennen, daß hier wieder die Tagseite hinter der Nachtseite auftaucht bzw. umgekehrt, was schon ein Hinweis auf die vorhandene starke Raumkrümmung ist, aber wirklich besonders sieht diese Position nicht aus. Und hier sollen tatsächlich Photonen rotieren können? Da hilft eigentlich nur eines: Wieder einmal `Gott' spielen und um die Erde herum entlang des Photon Orbit eine künstlichen Torus setzen, die man vielleicht als eine Art überdimensionale Raumstation interpretieren könnte. Der Mond, der sich ja auch auf dem Photon Orbit befindet, wird von diesem Torus, der sich um die Erde schlingelt, quasi aufgespießt. Bevor in dieser Szene nun aber die Gravitation `eingeschaltet' wird, heißt es, erst einmal auf einen genügenden Sicherheitsabstand zu gehen, sagen wir, sieben Erdradien Distanz. Und nun: `Klick' - mit Gravitation. Das Licht fällt auf immensen Spiralbahnen hinunter, wird unweigerlich von der Erdoberfläche angezogen und der Planet erscheint mit einem Mal in einer Größe, die den Bildausschnit sogar übersteigt. Durch die Raumkrümmung ändern sich natürlich auch die Entfernungen, und somit auch der Abstand zur Planetenoberfläche. Würde man jedoch in dieser Entfernung den Planeten umrunden wollen, bräuchte man dafür mit der gleichen Geschwindigkeit genauso lange wie im vorigen Bild des flachen Raumes - der Umfang ist bei gleichem Schwarzschildradialabstand (dem `Kugelflächenradius') der gleiche, diese Eigenschaft definiert die Schwarzschild-Radialkoordinate. Der wahre Abstand zur Planetenoberfläche ändert sich jedoch durch die Raumkrümmung. Um jetzt eine besseren Blick zu haben, ist es zweckmäßig, das Kameraobjektiv zu wechseln und ein Objektiv mit einem Bildwinkel von 120° (horizontal) zu verwenden. So paßt nun die gesamte gekrümmte Planetenoberfläche und der nahe umgebende Raum ins Bildfeld. Wieder sieht man, wie schon zuvor beschrieben, die gesamte Oberfläche auf einmal. Aber auch den Torus, der sich um den Planeten wickelt, kann man in seiner Gesamtheit sehen, er scheint sich über den Nordpol zu wickeln. Das ist insofern verständlich, weil sich der Beobachter etwas oberhalb der Äquatorebene befindet und daher das Licht über den Nordpol hinweg vom Torus zum Beobachter hin abgelenkt wird.

Doch nun wollen wir uns die ganze Angelegenheit einmal aus der Nähe ansehen. Setzen wir uns in ein Raumschiff, das in einem Abstand von zwei Erdradien etwas oberhalb der Äquatorebene positioniert wird. Im Nahebereich scheint der Torus `ganz normal' über der Erdoberfläche zu verlaufen, aber anstatt hinter dem Horizont zu verschwinden, wie man dies von unserer echten Erde erwarten würde, biegt er auf einmal steil nach oben ab, um dann über den Nordpol herum wieder `hinten' anzukommen. Der Bildausschnitt ist natürlich zu klein, um auch noch die Nordpol ein einem zu zeigen, aber nach den Erfahrungen mit den vorigen Bildern ist dieses Verhalten zu erwarten und auch einsichtig. Wie bereits gesagt: Man sieht ja die gesamte Oberfläche des Planeten, als wäre sie eine flache Scheibe. Hatten die Leute des Mittelalters also doch recht mit ihren Ansichten...?
Nun gut, wenn sich das Raumschiff oberhalb der Äquatorebene befindet, scheint der Torus nach oben hin abzuknicken, analoges geschähe, wenn sich das Raumschiff unterhalb der Äquatorebene befindet. Was aber, wenn man genau aus der Äquatorebene auf den Torus blickt? Dann kann er ja eigentlich aus Symmetriegründen weder nach oben noch nach unten abknicken...? Nun ist aber so ein Torus keine unendlich dünne Linie, sondern manche Teile liegen oberhalb, manche unterhalb der Äquatorebene. Teile, die oberhalb liegen, erscheinen daher nach oben abgelenkt, südliche Teile nach unten. Der Torus selbst scheint sich daher `zu teilen', über den gesamten Horizont zu erstrecken und den gesamten Horizont auszufüllen. Da der Torus selbst nur relativ klein ist, erscheint er daher, auf den gesamten Horizont ausgedehnt, extrem verzerrt. Man kann daran auch eine weitere Eigenschaft des Photon Orbit erkennen: Kreisbahnen des Lichts entlang des Photon Orbit sind nicht stabil, sondern äußerst labil - eine kleine Abweichung von der exakten Kreisbahn genügt, und das Photon spiralt entweder in das Schwarze Loch hinab oder kann in die Unendlichkeit des Weltalls entkommen.
Jetzt aber wollen wir unser Raumschiff direkt auf dem Photon Orbit plazieren, etwas oberhalb des Torus, sodaß man ihm entlang den Weg der Photonen verfolgen kann. Und tatsächlich: Der eigentlich um den Erdmittelpunkt gewickelte Torus erscheint vollkommen gerade, da sich das Licht parallel zur Krümmung des Torus ebenfalls um die Erde herum wickelt! Ab einer bestimmten Entfernung dann scheint der Torus wieder nach Norden abzubiegen, wie man das schon aus den vorherigen Bildern kennt. Hinter dem Rand der Erdoberfläche verschwinden kann er ja nicht, da es keinen Rand mehr gibt, wenn die gesamte Kugeloberfläche sichtbar ist, und sich im Unendlichen verlieren, wie eine unendlich lange Stange im flachen Raum, ist ebenfalls nicht möglich, da der Torus ja nur endlich lange ist.
Nun soll das Raumschiff noch etwas weiter nach innen gesteuert werden, hier etwas innerhalb des Photon Orbit, bei 1.4 Erdradien (=Schwarzschildradien). Der Torus scheint immer noch gerade zu sein, wenn nicht sogar schon etwas nach außen gekrümmt. Am Horizont der Erdscheibe taucht aber hinter der Nachtseite ein heller Streifen auf, ein Hinweis, daß man hier schon wieder die Tagseite `einmal herum' sehen kann, und sichtbares Anzeichen dafür, daß man sich hier in einem Bereich noch größerer Raumkrümmung befindet.
Und zuletzt noch ein Blick von nur 1% außerhalb des Schwarzschildradius. Sowohl die Erdoberfläche als auch der Torus scheinen nach außen gebogen, als würden sie bald `zusammenklappen'. Man ist dem Punkt nahe, aus dem es kein Entkommen mehr gibt.
Doch nun wieder einen Sprung zurück, zum Photon Orbit. Wenn dort Licht auf Kreisbahnen läuft, müßte es doch möglich sein, seinen eigenen Hinterkopf zu sehen? Da der Beobachter in Computersimulationen nicht wirklich sichtbar ist (oder nur mit großem Aufwand sichtbar gemacht werden kann), muß in diesem Fall als `Hinterkopf' der Mond herhalten, der ja auch immer noch da ist und nicht umsonst an die Position des Photon Orbits gesetzt wurde. Nur wurde eben bislang der Torus betrachtet und der Mond, der sich beim tangentialen Blick entlang des Torus genau hinter dem Beobachter befindet, außer acht gelassen. Aber tatsächlich, wenn man den Torus, der den Blick verdeckt hatte, wieder aus der Szene entfernt, erscheint in weiter Ferne ein Silberstreifen am Horizont, der der - extrem verzerrten - Rückseite des Mondes entspricht.
Dies ist so kein allzu eindrucksvolles Bild, weil der Mond zuwenig Struktur enthält, als daß man nach der Verzerrung entlang des Photon Orbit nach einer Erdumrundung noch etwas erkennen könnte. Genausogut könnte dies ein heller Fleck auf der Erdoberfläche sein. Also heißt es wieder einmal etwas Gott spielen und eine Lampe, in etwa eine rote Lichtkugel, auf der Rückseite des Mondes anzubringen, damit man etwas mehr erkennen kann. Das sieht dann im flachen Raum so aus wie in diesem Bild.
Das gleiche, im flachen Raum aufgenommene Bild im Detail, mit einem Bildausschnitt von horizontal 10°.
Nun die gleiche Anordnung wie zuvor, allerdings der Mond `nach hinten', gerade hinter den Beobachter versetzt. Bei einem Bildausschnitt von nur 1°, einem zehntel des vorigen, kann man nun am fernen Horizont wieder den Silberstreif erkennen, aber diesmal mit der roten Lampe, die in einen langen Strich gedehnt wird.
Nun noch ein noch schärferer Blick mit einem Blickwinkel von 0.1°. Wirkliche Strukturen kann man keine mehr sehen, dazu ist die Verzerrung zu stark, aber man kann erahnen, daß es die Lichtkugel ist, die auf der Rückseite des Mondes plaziert wurde, die man hier `einmal um die Erde herum' sieht. So also würde man seinen eigenen Hinterkopf auf dem Photon Orbit sehen. (Vgl. das analoge Bild im flachen Raum mit 10° Ausschnitt.)
Gut, und wenn Licht tatsächlich entlang des Photon Orbit rotieren kann, dann müßte man ja auch die Erdoberfläche nahe des Photon Orbit beliebig oft sehen können, denn das Licht kann ja die Erde mehr als einmal umrunden, bis es schließlich auf die Oberfläche hinabstürzt. Leider verdeckt der Mond selbst in den vorhergehenden Bildern den Blick entlang des Photon Orbits. Also setzen wir den Mond einfach auf eine etwas höhere Umlaufbahn und - voila! - tatsächlich taucht hinter der Nachtseite, die ja bereits hinter der Tagseite sichtbar ist, wieder die Tagseite auf. Es dürfte sich dabei um Indonesion handeln, das man so bereits `nach einer Lichtrotation' um die Erde herum das zweite Mal sieht. Das erste Mal erscheint Indonesien ja bereits nahe unterhalb des Beobachters, wie man etwa am Bild des tangentialen Blickes entlang des Torus in einem der vorigen Bilder sehen kann. Dieser Ausschnitt hier ist aber nur ein winzig kleiner Bereich von 1° entlang des Horizontes. Würde man noch kleinere Auschnitte wählen, könnte man wohl noch mehrfache Wiederholungen der gleichen geographischen Gebiete sehen, jede Wiederholung um ein Vielfaches verzerrter und winziger als die vorangegangenen. Wie bereits erwähnt, der Photon Orbit ist eine instabile Kreisbahn.

The End

* Der Tag, als die Erde zu einem Schwarzen Loch wurde: Genaugenommen war dies der 20. Juli 1997, der Tag, an dem die meisten dieser Simulationen berechnet wurden.