 As an starting point one needs a `virtual laboratory' with planet Earth inside.
Even better, the lab shall contain the Moon also, such that the scenery
isn't too trivial at all. In nature the moon resides at a distance
of about 60 times the radius of Earth, but in the virtual lab the experimentator
may `play the role of God' and set the Moon to a distance of a mere 1.5 times
the radius of Earth. This distance is called the Photon Orbit.
At the Photon Orbit light, i.e. photons, may rotate around the Black Hole
on an perfect circle. The visual effects resulting out of this behaviour will
be shown in the following images and descriptions.
As an starting point one needs a `virtual laboratory' with planet Earth inside.
Even better, the lab shall contain the Moon also, such that the scenery
isn't too trivial at all. In nature the moon resides at a distance
of about 60 times the radius of Earth, but in the virtual lab the experimentator
may `play the role of God' and set the Moon to a distance of a mere 1.5 times
the radius of Earth. This distance is called the Photon Orbit.
At the Photon Orbit light, i.e. photons, may rotate around the Black Hole
on an perfect circle. The visual effects resulting out of this behaviour will
be shown in the following images and descriptions.
 To improve realism of the situation the `lab desktop' is
preferably to be eliminated from the scene.
In reality the system of Earth and Moon is
embedded within the star-filled celestial background, and accordingly
in this next simulation image the Moon
is shining above the nocturnal central parts of Africa in front of the starry sky.
Its data were provided by the SAO catalogue of the 258.000 brightest stars
(compiled by the Smithsonian Astrophysical Observatory).
Data from the Earth's surface (day and night part) came from
Living Earth ®,
the Moon's surface has been constructed using data from the
US space probe Clementine.
To improve realism of the situation the `lab desktop' is
preferably to be eliminated from the scene.
In reality the system of Earth and Moon is
embedded within the star-filled celestial background, and accordingly
in this next simulation image the Moon
is shining above the nocturnal central parts of Africa in front of the starry sky.
Its data were provided by the SAO catalogue of the 258.000 brightest stars
(compiled by the Smithsonian Astrophysical Observatory).
Data from the Earth's surface (day and night part) came from
Living Earth ®,
the Moon's surface has been constructed using data from the
US space probe Clementine.
 The scene could be rendered even more realistic if the earth's atmosphere
is taken into account also (which is enlarged here by a factor of 15 as
compared to its true extension). Please note the appearance of the atmospheric
reddening at the poles near the terminator, demonstrating the aurora as seen
from space. Unfortunately the addition of atmospherical effects
increases computation time by a factor of 60.
Therefore the succeeding simulations have been made `in vacui'.
The scene could be rendered even more realistic if the earth's atmosphere
is taken into account also (which is enlarged here by a factor of 15 as
compared to its true extension). Please note the appearance of the atmospheric
reddening at the poles near the terminator, demonstrating the aurora as seen
from space. Unfortunately the addition of atmospherical effects
increases computation time by a factor of 60.
Therefore the succeeding simulations have been made `in vacui'.
Now, what happens, if Earth had such an mass, that it would enclose 90% of its Schwarzschild radius? This percentage is near stability limit of a static star; the exact value is 9/8 of the Schwarzschild radius, which corresponds to a fill rate of 88%. If any object is compactified within a volume smaller than this limit, it will inevitably collapse even further due to its own gravitational field, finally ending as a Black Hole.
 The gravitational field of such an compact object is of such
an intensity that light rays are `bended downwards' towards the mass.
A light ray, which in flat space would pass straight ahead over the north pole,
would be attracted by the gravitation and `fall down' to the the north pole.
Therefore the north pole - and even the regions beyond - become visible for an
observer residing in the equator plane. The same happens to the south pole,
which becomes visible also, contained within the same view of the north pole.
The gravitational field of such an compact object is of such
an intensity that light rays are `bended downwards' towards the mass.
A light ray, which in flat space would pass straight ahead over the north pole,
would be attracted by the gravitation and `fall down' to the the north pole.
Therefore the north pole - and even the regions beyond - become visible for an
observer residing in the equator plane. The same happens to the south pole,
which becomes visible also, contained within the same view of the north pole.
Similar conditions are valid at the equatorial plane: The light is bent around the Earth and therefore the full day side can be seen at once together with the full night side; moreover beyond the night side the day side becomes visible again, since the light has made one `turn around the Earth', and similarly somewhat right of the day side the night side is visible for the second time. Effectively one is able to watch the complete surface of a Black Hole at once (and even more than once).
But to be correct it has to be stated that the simulation shown here is wrong in some aspect. If it is possible to see the entire surface from any location, then it is also possible to see the entire celestial sphere from any location on the surface. Therefore the sun were visible from any surface location, because the light coming from the sun would also be attracted to parts of the Earth's surface which are unreached by the sunlight in flat space, i.e. the former nocturnal hemisphere. The distinction between night and day becomes meaningless under such conditions, the sun is shinig everywhere at the same brightness. This influence of the space curvature to the infalling light was not taken into account for the simulations presented here, on the one hand, because this were quite complicated to be done computationally, on the other hand, because this method of - `false' - visualization enables a more intuitive and impressive view of the difference between front side and back side.
 Now what would an observer see, who is residing within the curved space,
not just looking at it from outside at save distances?
This image shows the view to the moon, seen from a radial distance from Earth
of 1.1 radii, i.e. .1 Earth radii above the surface (ca. 600km).
The strange look is obvious: the Moon seems to be stretched to become an
elliptical shape, the starry sky also appears to be somewhat `crunched'
near the horizon - as stated earlier, one is able to see the complete sky from
any point on the surface, because the star light is spiralling inwards from
any direction. Moreover the entire surface is visible from any
point within the surface itself, since light rays, which can't escape
from the surface due to their zenith angles beeing too large,
will be attracted back to the
Earth's surface. For that reason the sunward side (`day side') appears
behind the night side near the horizon, somewhat below the Moon.
Now what would an observer see, who is residing within the curved space,
not just looking at it from outside at save distances?
This image shows the view to the moon, seen from a radial distance from Earth
of 1.1 radii, i.e. .1 Earth radii above the surface (ca. 600km).
The strange look is obvious: the Moon seems to be stretched to become an
elliptical shape, the starry sky also appears to be somewhat `crunched'
near the horizon - as stated earlier, one is able to see the complete sky from
any point on the surface, because the star light is spiralling inwards from
any direction. Moreover the entire surface is visible from any
point within the surface itself, since light rays, which can't escape
from the surface due to their zenith angles beeing too large,
will be attracted back to the
Earth's surface. For that reason the sunward side (`day side') appears
behind the night side near the horizon, somewhat below the Moon.
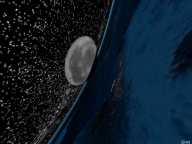 But in a virtual lab there is no reason counting against the idea to
have the mass of Earth beeing increased up to the Schwarzschild limit.
A Schwarzschild radius of about 6000km, as it is the Earth's radius,
corresponds to about 2500 masses of the sun (which by itself has an
Schwarzschild radius of about. 2.5km), which had to be compressed
to fit within the volume of the Earth. Such an object isn't physically
stable any more, nethertheless it can be simulated in spite of that.
The appearance compared with the former simulation isn't
very distinctive, the bending tr the horizon becomes somewhat stronger,
also becomes the distorsion of the moon and the starry sky.
But in a virtual lab there is no reason counting against the idea to
have the mass of Earth beeing increased up to the Schwarzschild limit.
A Schwarzschild radius of about 6000km, as it is the Earth's radius,
corresponds to about 2500 masses of the sun (which by itself has an
Schwarzschild radius of about. 2.5km), which had to be compressed
to fit within the volume of the Earth. Such an object isn't physically
stable any more, nethertheless it can be simulated in spite of that.
The appearance compared with the former simulation isn't
very distinctive, the bending tr the horizon becomes somewhat stronger,
also becomes the distorsion of the moon and the starry sky.
 However one should note that this is one of the last seconds in the life
of an observer falling into a Black Hole.
From this location
he might still escape with some powerful spacecraft (Warp drive should do it),
but a couple of steps towards the center, and any chance to escape gets lost
forever. There is no way to leave the region within the event horizon
(within the Schwarzschild radius).
However one should note that this is one of the last seconds in the life
of an observer falling into a Black Hole.
From this location
he might still escape with some powerful spacecraft (Warp drive should do it),
but a couple of steps towards the center, and any chance to escape gets lost
forever. There is no way to leave the region within the event horizon
(within the Schwarzschild radius).
The `last glimpse' to the Moon could look like this image: The falling astronaut (or kosmonaut) has approached the event horizon as near as mere 10km. Similarly some mountaineer on a somewhat heightened Mt. Everest within the central Sahara could see the same (if one neglects the influence of special relativity effects due to different motion of these two observers, i.e. the astronaut should not be in free fall, but somehow rest at a constant radial distance).
But now let's go back somewhat outwards, up to the more interesting
regions around the Photon-Orbit, which was mentioned already.

 At first impression this position doesn't appear very exciting.
Neither the view towards the Moon, nor the view in the opposite direction
seem to be very particuliar. Again, the stars become more and more distorted
near the horizon, and, as before, the day side is visible beyond the night
side and vice versa, which is a hint to the strong curvature of space at
this place, but it doesn't look too interesting at all.
Could this really be the region of rotating photons?
At first impression this position doesn't appear very exciting.
Neither the view towards the Moon, nor the view in the opposite direction
seem to be very particuliar. Again, the stars become more and more distorted
near the horizon, and, as before, the day side is visible beyond the night
side and vice versa, which is a hint to the strong curvature of space at
this place, but it doesn't look too interesting at all.
Could this really be the region of rotating photons?
 But there is a solution to stop disappointment because of this `boring'
appearance: Let's play God again and set an artificial torus around the Earth,
just at the radius of the Photon Orbit. One may consider this torus as
some kind of `hyperfinanced space station' (it's a simulation!).
The Moon, residing at the Photon Orbit also, becomes therefore be
`pierced' by this torus.
But there is a solution to stop disappointment because of this `boring'
appearance: Let's play God again and set an artificial torus around the Earth,
just at the radius of the Photon Orbit. One may consider this torus as
some kind of `hyperfinanced space station' (it's a simulation!).
The Moon, residing at the Photon Orbit also, becomes therefore be
`pierced' by this torus.
 Before `switching on' gravitation, it's better to go to some greater
`safety' distance, say, seven times the radius of Earth.
Before `switching on' gravitation, it's better to go to some greater
`safety' distance, say, seven times the radius of Earth.
 But now: `Click' - gravitation switched on.
Light falls down on large spiral-like paths, is inevitably beeing attracted
by the Earth's mass and the whole planet appears to be of an size
which even extends the current field of view. Space curvature changes
distances, and so it does change the distance to the planet's surface.
However a spaceship orbiting the planet at the same speed and at the same
distance as in the previous image (in flat space) would need exactly the
same time to do so - the circumference at a certain radial distance
doesn't change at equal Schwarzschild radial distance. It is just this property
of the Schwarzschild radial distance which defines it.
Nethertheless the true (metric, measurable) distance to the
planet's surface is changed by the space curvature.
But now: `Click' - gravitation switched on.
Light falls down on large spiral-like paths, is inevitably beeing attracted
by the Earth's mass and the whole planet appears to be of an size
which even extends the current field of view. Space curvature changes
distances, and so it does change the distance to the planet's surface.
However a spaceship orbiting the planet at the same speed and at the same
distance as in the previous image (in flat space) would need exactly the
same time to do so - the circumference at a certain radial distance
doesn't change at equal Schwarzschild radial distance. It is just this property
of the Schwarzschild radial distance which defines it.
Nethertheless the true (metric, measurable) distance to the
planet's surface is changed by the space curvature.
 To have a better overview it is required to use another camera lens,
e.g. one with an
horizontal view angle of 120° instead of 50° as before.
So the full distorted surface and the near space arround fits into the view field.
Again, the entire surface of the planet is visible.
But also the torus, which is wound around the Earth at the equatorial plane,
is visible at each point of its course. The torus seems to be laid
around the north pole. This is easy to understand, since the observer is
residing somewhat above the equatorial plane and light rays originating
from the torus are bent downwards towards the north pole,
finally entering the observer's eye.
To have a better overview it is required to use another camera lens,
e.g. one with an
horizontal view angle of 120° instead of 50° as before.
So the full distorted surface and the near space arround fits into the view field.
Again, the entire surface of the planet is visible.
But also the torus, which is wound around the Earth at the equatorial plane,
is visible at each point of its course. The torus seems to be laid
around the north pole. This is easy to understand, since the observer is
residing somewhat above the equatorial plane and light rays originating
from the torus are bent downwards towards the north pole,
finally entering the observer's eye.










