|
This information has also been published in
F.W.Hehl, R.A.Puntigam, H.Ruder (Eds.) |
Astronomy site of the day 9/19/96 |
Newtonian Simulation (186KB) |
Einsteinian Simulation (227KB) |
Both images show a complex scenery, which should enable the viewer to get some intuitive feeling for the curvature of space, which is, according to Einsteins theory of General Relativity, caused by the existence of mass. The "Newtonian simulation" shows a view over the sea and a spherical mass hovering above it with a soccerball-like shape. Its gravitational force attracts the water below and creates a tiny hill of water. The arising 'drop' is just under this mass. Diagonally pointing to the backside there is a white bar, which should clearify the spatial context of the objects. The backward end of this bar hits a ikosaeder, which is shining in red light. This light also enlightens the backside of the spherical mass; this effect is partially visible on the sphere's right side. Further behind at the distance of the brick cylinder with its flattened balls of gold there resides the tilted cylinder with its black and red colored surface. The influence of the curvature of space on this scene will be described detailed in the following text.
Its the basic idea of the Theory of General Relativity that mass will change space curvature and therefore light rays will follow another path than in flat (euclidean) space. As the path of a fast moving particle is bend by some massive object, light rays move "around a mass".
The most simple case is known as the Schwarzschild-Solution, which
describes the vacuum field of a spherical symmetric, nonrotating
and uncharged amount of mass. It is a particularity of this solution
to have an event horizon, if the source mass is concentrated
within the Schwarzschild-Radius
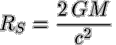
A ray of light is bend by some mass with a Schwarzschild-Radius
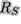by an angle
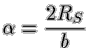
, where b denotes the minimal distance of the ray to the bending
mass:
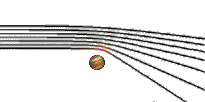
Its one unusual property that some object may be seen by an observer
more tha once, e.g. the shining ikosaeder or the brick cylinder with
its flattened golden balls; this effect may be imagined easy, since
light rays may reach the observer's eye using different paths:
 (inverse, small) |
 (normal position, distorted) |
If there is an object exactly behind the gravitational lens, then there
are no more two images ("inside" and "outside"), but both images get
molten to a ring with the gravitational lens in its center.
This phenomena is also known as the Ring of Einstein and has
been observed in nature (at least approximative).
The oberver now resides quasi in the "focus" of the lens, one point
on the object's surface is visited as a lineshape image and therefore
maximally enlarged.
In this simulation this object point is part of the tilted black and
red sprinkled cylinder; the simulation also shows, that continuos
surface structures are distorted more and more, the nearer they
come to the inversion radius - until they finally become formed
like the inversion radius itself and construct the Einstein Ring.
All these phenomenas, which are connected to the Einstein Ring, have already been observed in nature, although their scale is much smaller; Beams are bend by some degrees in this simulation, but modern astronomical observations show a typical scale of 15 arc seconds.
|
|
The event horizon can't be visible itself, since no light may escape to outside from there. Netheretheles one may imagine the event horizon surrounded by a thin membrane, which may send light to the outside world. The light originating from this membrane therefore enables the observer to catch some impressions from the space just outside the event horizon. In reality any light would get extremely reddened by the gravitional field, so that the surface structure of the membrane could merely be seen in red or infrared light (and therefore possibly be unvisible). The gravitational redshift was explicitely excluded in this simulation because of this effect.
Near the event horizon there are phenomenas, which are completely unusual: controversely to great distances, where the path of light rays may rawly be described by hyperbolas, this approximation is no longer valid at smaller distances. There the light rays may be bend in such a strong kind, that it turns back to the light source, or, expressed in another way, the observer may spectate himself. At less distances to the event horizon there is a region, there the light may encircle the Black Hole or even get stuck in an orbit ("photon orbit"). The more the observer's view direction approximates this photon orbit, the more often (and smaller) the whole outer world is been mapped spherically, additionally to the effects of gravitational lensing mentioned above.
|
Finally, looking inside the photon orbit, all light rays are bend so strong that they unavoidable touch the "surface" of the Black Hole (the covering membrane). Outer rays are slowly spiralling inwards, orbiting the Black Hole more than once, whereas rays, which are aimed directly to the Black Hole's center, hit the surface nearly without bending. The Black Hole's side lying in front of the observer therefore seems to be visible nearly without distortions, but soon one will become aware, that also the "north pole" of the ball is visible (as is the south pole, but this one is without light and therefore to dark to be seen). The light (equivalent to the view path of the observer) quasi spirals from the top down to the pole and beyond to the backside. Now also the part of the ball, which is enlightened by the red ikosaeder from behind, becomes visible - the observer is able to see not only one side of the black hole (as it is known from experience), but he may see the whole surface area! This might be unusual enough, but additionally the whole surface is not only visible from one point of view, but from any point of view!
|
The calculations presented here were done in March 1993 on the workstations of the EDV-Pool. The Einsteinian simulation used seven hours in a parallelized raytracing programg on three HP-workstations - extrapolated to a PC's power, an 386/33 MHz would need about two months to do the same...
Please feel free to send me any comments, including remarks to mispelling or unfortunately bad english.
Virtual Trips to Black Holes and Neutron Stars
Another interesting effect, which profits from the spatial structure of
the scene, may be seen with the desk of wood, which is used as fundament
for the ikosaedric light source:
Controversary to the newtonian simulation, where only the upper side
of the desk is visible, the curvature of space also enables the observer
to have a glimpse to the left edge of the downward side, where the
curvature is stronger than on the right edge. Light originating
from the downward side is bend by the gravitational active mass
upwards and therefore may reach the observer's eye. The desk itself
seems to be totally distorted, though it is absolute plane in its
real position as it was before in the newtonian simulation.
