4.6 Spezielle Eigenschaften der Schwarzschildmetrik
4.7 Der Ereignishorizont
Eine Hyperfläche ist durch eine Funktion f:M\mapsto\Bbb R
festgelegt, sodaß auf der Hyperfläche gilt:
f(x^\mu) = \mbox{const.}
Der Normalvektor auf diese Fläche ergibt sich aus dem
vierdimensionalen Gradienten:
n = n^\nu \partial_\nu = g^{\nu\mu} f,_\mu \partial_\nu
Eine Hyperfläche wird Nullhyperfläche genannt, wenn gilt
G(n,n) = 0
in jedem Punkt der Hyperfläche, d.h. der Normalvektor n ist lichtartig und
daher orthogonal zu sich selbst;
somit ist der Normalvektor auf die Nullhyperfläche gleichzeitig auch tangential,
Tangential- und Normalvektoren sind auf der Nullhperfläche identisch.
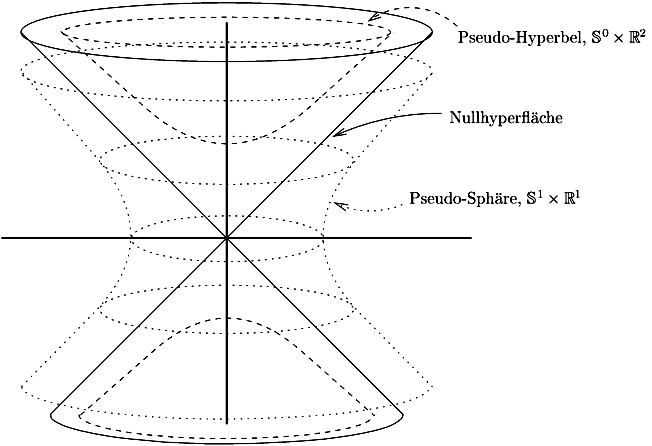Im Minkowski-Raum stellt die Fläche x=\pm t bzw.
f=x\mp t
eine Nullhyperfläche mit dem Normalenvektor n=(1,-1,0,0)
und \eta(n,n)=0
dar. Die Zukunftslichtkegel liegen alle auf einer Seite der Hyperfläche,
in die Zukunft gerichtete zeitartige Weltlinien können die
Nullhyperfläche nur in einer Richtung durchqueren.
Eine Nullhyperfläche, die sich nicht ins räumlich Unendliche erstreckt,
nennt man einen Ereignishorizont.
Im Schwarzschildfall bildet die Fläche r=2m einen Ereignishorizont
mit dem Normalenkovektor \left.dr\right|_{r=2m}
und g(dr,dr)=g^{rr}\equiv g_{tt}=0.