4.8 Eddington-Finkelstein-Koordinaten
Die Schwarzschild-Radialkoordinate ist über den Kreisumfang definiert:
Ein relativ zur gravitativ wirkenden Masse ruhender Beobachter messe
den Kreisumfang aller Punkte gleichen Radialabstandes (was z.B. durch
Bestimmung der lokalen Raumkrümmung geschehen könnte).
Die Radialkoordinate r ist dann so
definiert, daß sich der Kreisumfang
als 2\pi r ergibt. Gleichermaßen kann auch die Kugeloberfläche
mit dem Wert 4\pi r^2 vermessen werden;
für eine Radialkoordinate mit dieser Eigenschaft wird in der Folge
die Bezeichnung `Kugelflächenradius' verwendet.
Vergleicht ein ruhender Beobachter seine Kreisumfangsmessung
mit einem im zu ihm relativen Radialabstand
ds=dr/\sqrt{1-\frac{2m}{r}}
ruhenden Beobachter, so beträgt die Differenz der Meßergebnisse
2\,\pi\, dr = 2\,\pi\,ds\, \sqrt{1-\frac{2m}{r}}
D.h. je näher ein ruhender Beobachter dem
Schwarzschildradius r=2m
kommt, desto weniger ändert sich der von ihm gemessene Kreisumfang,
im Extremfall r=2m bewirkt jede beliebige Änderung des
Radialabstandes ds keine Änderung des Kugelflächenradius;
selbst eine unendlich starre kugelförmige Hülle könnte bei
r=2m
beliebig radial verschoben werden, da sich durch diese radiale
Verschiebung die Oberfläche und folglich eine daraus resultierende
Oberflächenspannung nicht ändern würde. Tatsächlich jedoch wäre
ein `Herausziehen' der Hülle mit erheblich mehr Energieaufwand
verbunden, da man ja gegen das Gravitationspotential
ankämpfen müßte - nur die Gegenkräfte aufgrund einer Oberflächenspannung
würden fortfallen. In Summe ist nur das `Hineindrücken' ohne
weiteres möglich bzw. würde von selbst erfolgen. Letztlich bedeutet dies,
daß auch eine unendlich starre Membran am Schwarzschildradius
unaufhaltsam weiter hinein gezogen würde.

Da es bei r=2m keine ruhenden Beobacher mehr gibt, ist es nicht
verwunderlich, daß die Schwarzschildmetrik dort singulär wird.
Ein frei fallender Beobachter erreicht jedoch die
Singularität bei r=0
in endlicher Eigenzeit und mißt infolgedessen auch einen endlichen
Radialabstand. Daher ist es sinnvoll, die Schwarzschildmetrik in
Koordinaten auszudrücken, die einem bewegten Beobachter angepaßt sind.
Die einfachste Möglichkeit besteht darin, die Metrik lichtartigen
Geodäten anzupassen (radial einfallenden Photonen).
Wegen ds=0 und
d\Omega=0 gilt:
\left( 1 - \frac{2m}{r} \right) dt^2 = \frac{dr^2}{1-\frac{2m}{r}}
bzw.
dt = \pm\frac{dr}{1-\frac{2m}{r}}
Für einfallendes Licht wird mit größerem t die
Radialkoordinate r kleiner,
daher gilt `-' bzw.
dv := dt + \frac{dr}{1-\frac{2m}{r}} = 0
Dieser Ausdruck legt die Einführung einer avancierten
Lichtkoordinate v
nahe:
v = t - \int dt
= t + \int \frac{dr}{1-\frac{2m}{r}}
= t + ( r + 2m \ln | r - 2m | )
Einfallende Lichtstrahlen bewegen sich entlang
dv=0 bzw. v=const. const.
Über diese Lichtkoordinate kann wiederum eine neue - avancierte - Zeitkoordinate
definiert werden:
\bar t := v - r = t + 2m \ln | r - 2m |
Wegen v=const. bleibt \bar t
endlich für r\rightarrow 2m, während
t\rightarrow\infty.
Nun gilt
d\bar t = dv - dr = dt + \frac{dr}{ 1 - \frac{2m}{r} } - dr
= dt - dr \left( 1 - \frac{1}{ 1 - \frac{2m}{r} } \right)
= dt - \frac{dr}{1-\frac{r}{2m}}
(Vgl. Straumann) bzw.
dt^2 = d\bar t^2
+ \frac{2}{ 1 - \frac{r}{2m} } d\bar t dr
+ \frac{1}{ \left( 1 - \frac{r}{2m} \right)^2 } dr^2
Somit ergibt sich für die Metrik:
ds^2 = \left( 1 - \frac{2m}{r} \right ) d\bar t^2
+ 2 \frac{ 1 - \frac{2m}{r} }{ 1 - \frac{r}{2m} } d\bar t dr
+ \frac{ 1 - \frac{2m}{r} }{ \left( 1 - \frac{r}{2m} \right)^2 } dr^2
- \frac{1}{ 1 - \frac{2m}{r} } dr^2
- r^2 d\Omega^2
Nebenrechnungen:
\frac{ 1 - \frac{2m}{r} }{ 1 - \frac{r}{2m} } =
\frac{ 1 - \frac{2m}{r} }
{ \frac{r}{2m} \left( \frac{2m}{r} - 1 \right) }
= - \frac{2m}{r}
\frac{ 1 - \frac{2m}{r} }{ \left( 1 - \frac{r}{2m} \right)^2 }
- \frac{1}{ 1 - \frac{2m}{r} }
=
\frac{ 1 - \frac{2m}{r} }
{
\left( \frac{r}{2m} \right)^2
\left( 1 - \frac{2m}{r} \right)^2
}
- \frac{1}{ 1 - \frac{2m}{r} }
=
\frac{1}
{
\left( \frac{r}{2m} \right)^2
\left( 1 - \frac{2m}{r} \right)
}
- \frac{1}{ 1 - \frac{2m}{r} }
=
\frac{1}{ 1 - \frac{2m}{r} }
\left[ \frac{1}{ \left( \frac{r}{2m} \right)^2 } - 1 \right]
=
=
\frac{1}{ 1 - \frac{2m}{r} }
\left[ \left( \frac{2m}{r} \right)^2 - 1^2 \right]
=
\frac{1}{ 1 - \frac{2m}{r} }
\left( \frac{2m}{r} - 1 \right)
\left( \frac{2m}{r} + 1 \right)
=
- \left( \frac{2m}{r} + 1 \right)
Die Schwarzschildmetrik nimmt daher in Eddington-Finkelstein Koordinaten
die Form
\boxed{
ds^2 = \left( 1 - \frac{2m}{r} \right) d\bar t^2
- \frac{4m}{r} d\bar t dr
- \left( 1 + \frac{2m}{r} \right) dr^2
- r^2 d\Omega^2
}
an. Die Metrik ist hier bei r=2m nicht
mehr singulär, dafür weist
sie jedoch nichtdiagonale Elemente auf (die andeuten, daß die Metrik
einem bewegten Beobachter angepaßt ist, hier radial einfallenden
Photonen).
Für radiale (d\Omega=0) Lichtstrahlen
(ds=0) gilt:
\left( 1 - \frac{2m}{r} \right) d\bar t^2
- \frac{4m}{r} d\bar t dr
- \left( 1 + \frac{2m}{r} \right) dr^2 = 0
Über die Umformungen
\left( 1 - \frac{2m}{r} \right) d\bar t^2
+ \left[
\left( 1 - \frac{2m}{r} \right)
-
\left( 1 + \frac{2m}{r} \right)
\right]
d\bar t dr
- \left( 1 + \frac{2m}{r} \right) dr^2 = 0
\left( 1 - \frac{2m}{r} \right) (d\bar t + dr) d\bar t
- \left( 1 + \frac{2m}{r} \right) (d\bar t + dr) dr = 0
folgt:
(d\bar t + dr)
\left[ \left( 1 - \frac{2m}{r} \right) d\bar t
- \left( 1 + \frac{2m}{r} \right) dr
\right]
= 0
Radiale lichtartige Geodäten können somit auf zweierlei Weise auftreten:
-
d\bar t + dr = 0 oder
dr = -d\bar t bzw.
\frac{dr}{d\bar t}=-1.
Die `Innenseite' des Lichtkegels ist, wie im Minkowski-Fall,
immer um 45o nach innen geneigt.
-
\left( 1 - \frac{2m}{r} \right) d\bar t - \left( 1 + \frac{2m}{r} \right) dr = 0
oder
\frac{dr}{d\bar t} = \frac{ 1 - \frac{2m}{r} }{ 1 + \frac{2m}{r} }
= \frac{r-2m}{r+2m}
=
\begin{cases}
r = \infty &: \ 1 \\
r = 2m &: \ 0 \\
r = 0 &: -1
\end{cases}
D.h. die `Außenseite' des Lichtkegels ist im unendlichen, wie im
Minkowski-Fall, unter 45o nach außen geneigt. Am Schwarzschildradius
r=2m liegt die
Außenseite parallel zur Zeitachse (\bar t) und
ist im Zentrum (r=0) identisch mit der Innenseite.
Die Darstellung der Schwarzschildlösung in Eddington-Finkelstein-Koordinaten
hat die Eigenschaft, nicht mehr zeitsymmetrisch zu sein.
In der Metrik kann statt `+' auch `-' gewählt werden,
anstelle einer avancierten also eine retardierte Zeitkoordinate
eingeführt werden. Daraus folgt eine zur Schwarzschildmetrik ebenfalls
isometrische Vakuumlösung, in der r=2m zwar auch eine Nullhyperfläche
darstellt, mit dem Unterschied jedoch, daß zeitartige Geodäten den
Ereignishorizont nur verlassen können (`Weißes Loch'-Lösung).
Beide Erweiterungen der Schwarzschildmetrik
(`Schwarzes Loch' und `Weißes Loch') können in einem durchgeführt
werden und führen zur maximalen Erweiterung der Schwarzschildlösung.
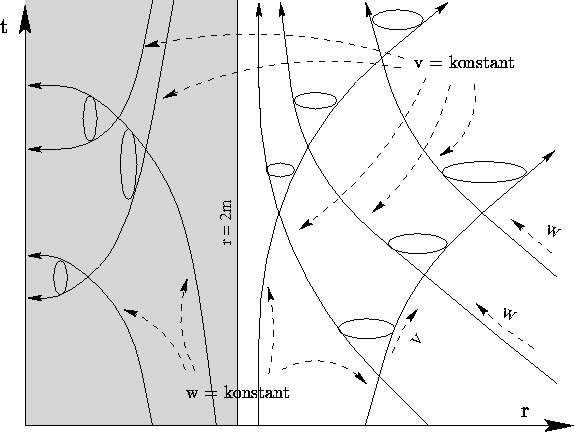
Geodäten und Lichtkegel eines statischen Schwarzen Loches in
Schwarzschildkoordinaten; einfallende Lichstrahlen laufen entlang den
v=const. Linien und scheinen bei
t=+\infty den Schwarzschildhorizont
r=2m zu erreichen, um
dann - von außen nicht feststellbar - aus dem
Unendlichen kommend `rückwärts' zur Singularität zu laufen. Der
Übergang bei r=2m ist in der Schwarzschildkarte nicht darstellbar.
Wegen der Unzulänglichkeit dieser Karte tritt auch der seltsame
anmutende Effekt auf, daß der Zukunftskegel für r<2m
nach r=0 gerichtet
erscheint - die Schwarzschild-r-Koordinate ist dort zeitartig.
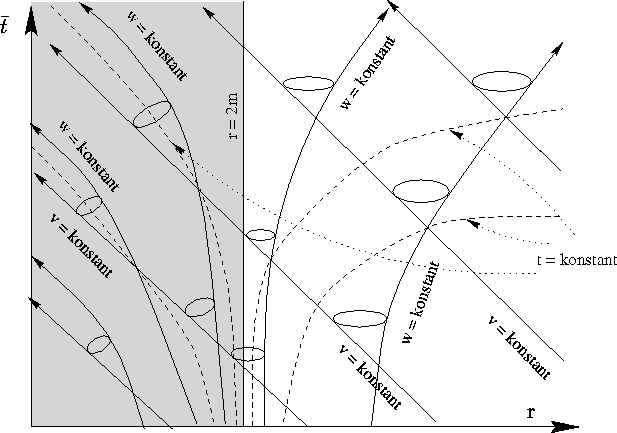
Geodäten und Lichtkegel eines statischen Schwarzen Loches in
Eddington-Finkelstein-Koordinaten. Die Karte ist den einlaufenden
Lichtstrahlen angepaßt, sodaß die v=const.
Linien als 45o-Geraden
dargestellt werden. Dafür geht jedoch die Zeitsymmetrie (im Gegensatz
zur Schwarzschildkarte) verloren; eine waagrecht gespiegelte Darstellung
stellt genauso eine sphärisch symmetrische Vakuumlösung dar, ist jedoch
nur für r>2m ident mit der
ungespiegelten Lösung (`Weißes Loch'-Lösung).



