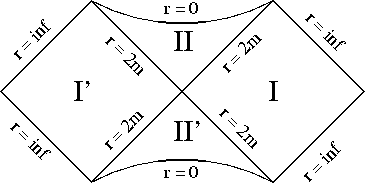4.9 Maximale Erweiterung der Schwarzschildlösung
Die Minkowskimetrik kann durch die Einführung lichtartiger Koordinaten v,w
v = t + x \qquad w = t - x
auf die Form
ds^2 = dt^2-dx^2-dy^2-dz^2 = dv\ dw - dy^2-dz^2
gebracht werden.
Analog können auch hier lichtartige Koordinaten eingeführt werden
(vgl. 4.8):
v := t + \int dt =\bar t + r = t + ( r + 2m \ln | r - 2m | )
Damit folgt direkt:
\bar t = v - r
\qquad
d \bar t = dv - dr
\qquad
d \bar t^2 = dv^2 - 2 dv\ dr + dr^2
Aus der Metrik in Eddington-Finkelstein Koordinaten wird damit:
ds^2
= \left( 1-\frac{2m}{r} \right) \left[ dv^2 - 2 dv\ dr + d r^2 \right]
- \frac{4m}{r} (dv-dr) dr
- \left( 1 + \frac{2m}{r} \right) dr^2 - r^2 d\Omega^2
= \left( 1-\frac{2m}{r} \right) dv^2 - 2 dv\ dr + r^2 d\Omega^2
Parallel zur avancierten Lichtkoordinate v kann eine retardierte
Lichtkoordinate w eingeführt werden:
w := t - \int dt
= t - \int \frac{dr}{1-\frac{2m}{r}}
= t - ( r + 2m \ln | r - 2m | )
Die Metrik, mithilfe der retardierten Lichtkoordinate w geschrieben,
hat die Form
ds^2 = \left( 1-\frac{2m}{r} \right) dw^2 + 2 dw\ dr + r^2 d\Omega^2
und beschreibt das `Weiße Loch'.
Zwischen dv, dw, dt und dr gelten die Beziehungen:
dv = dt + \frac{dr}{1-\frac{2m}{r}}
\qquad
dw = dt - \frac{dr}{1-\frac{2m}{r}}
und umgekehrt:
dv + dw = 2 dt
\qquad
dv - dw = \frac{ 2 dr }{ 1 - \frac{2m}{r} }
Damit kann dr ausgedrückt werden:
2 dr = (dv - dw) \left( 1-\frac{2m}{r} \right)
daher auch:
-2 dv\ dr = - \left( 1-\frac{2m}{r} \right) dv^2
+ dv\ dw \left( 1-\frac{2m}{r} \right)
Die Metrik nimmt nun in den Lichtkoordinaten
{v, w, \vartheta, \varphi} die einfache Form
ds^2 = - \left( 1-\frac{2m}{r} \right) dv\ dw + r^2d\Omega^2
an, wobei r(v,w) implizit über die Beziehung
\frac{v-w}{2} = r + 2m \ln | r - 2m |
und t(v,w) über
t = \frac{v+w}{2}
gegeben ist.
Neben dieser `Drehung' des Koordinatensystems (t,r)\rightarrow(v,w)
kann nun noch eine Streckung entlang der lichtartigen Koordinatenachsen
ausgeführt werden, sodaß die Lichtkegel in dem neuen Koordinatensystem
eine der Minkowski-Metrik identische Gestalt annehmen. Dazu werden
die Kruskal-Szekeres-Koordinaten \bar v, \bar w eingeführt:
\bar v := e^{v/4m}
\qquad
\bar w := - e^{-w/4m}
Es ergibt sich:
dv\ dw = \frac{\partial v}{\partial \bar v}
\frac{\partial w}{\partial \bar w}
d\bar v\ d\bar w
=
\left[ \frac{1}{4m} e^{v/4m} \frac{1}{4m} e^{-w/4m} \right]^{-1}
d\bar v\ d\bar w
\\
=
\left[ \frac{1}{16m^2} e^{ (v-w)/2 \frac{1}{2m}} \right]^{-1}
d\bar v\ d\bar w
=
\left[ \frac{1}{16m^2} e^{r/2m} e^{\ln(r-2m)} \right]^{-1}
d\bar v\ d\bar w
=
\left[ \frac{1}{16m^2} e^{r/2m} r (1-\frac{2m}{r}) \right]^{-1}
d\bar v\ d\bar w
= \frac{16 m^2}{r} e^{-r/2m} \frac{1}{1-\frac{2m}{r}}
d\bar v\ d\bar w
Die Schwarzschildmetrik hat also in Kruskal-Szekeres-Koordinaten die Form
\boxed{
ds^2 = \frac{16 m^2}{r} e^{-r/2m}
d\bar v\ d\bar w + r^2d\Omega^2
}
Durch eine weitere Drehung (\bar v,\bar w)\rightarrow(\bar t,\bar x)
kann die Koordinatendarstellung wieder der üblichen Darstellung angepaßt
werden.
Die Kruskal-Szekeres-Koordinaten haben den Vorteil, daß sich
lichtartige Geodäten wie bei der Minkowskimetrik an jedem Punkt als
45o--Geraden
darstellen lassen. Koordinatenlinien mit konstanter Schwarzschildzeit t
sind ebenfalls Geraden und laufen durch den Ursprung des Koordinatensystems,
wobei ein bestimmtes t zweifach in Erscheinung tritt - sowohl als
raumartige (bei r<2m) wie auch als zeitartige (bei r>2m) Koordinatenlinie.
Linien mit konstantem
r scheinen als Hyperbeln auf, der Ereignishorizont r=2m als durch
den Ursprung laufende Geraden (entartete Hyperbeln).
Die Singularität r=0 wird ebenfalls
als Hyperbel abgebildet (Vgl. Abbildung, Darstellung frei nach Hawking).
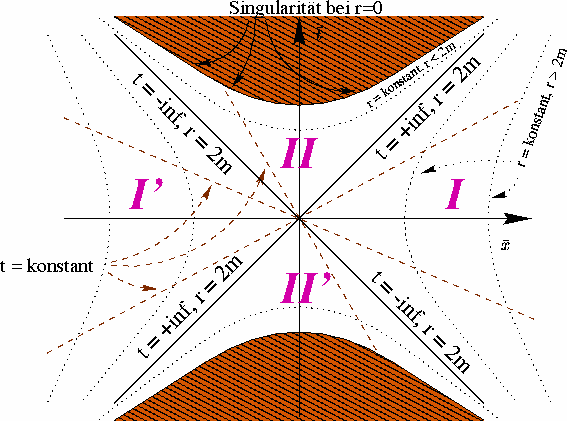
Kruskal-Diagramm. Vergangenheits- und Zukunftskegel werden an jedem
Punkt - wie in der Minkowski-Metrik - durch 45o-Geraden gebildet.
Beachtenswert ist, daß die Schwarzschild-Zeitkoordinate in der Region
I' scheinbar rückwärts läuft.
|
In der Kruskal-Szekeres-Darstellung der gesamten Schwarzschild-Mannigfaltigkeit
lassen sich vier Regionen
unterscheiden: Region I ist isometrisch zu der von der gewöhnlichen
Schwarzschildmetrik dargestellten Mannigfaltigkeit, Region I+II sind
isometrisch zur avancierten Eddington-Finkelstein-Lösung, während
Regionen I+II' isometrisch zur retardierten Lösung sind. Zusätzlich existiert
eine Region I', die ebenfalls isometrisch zur Schwarzschildlösung ist;
es gibt jedoch keine zeitartigen oder lichtartigen Verbindungslinien
zwischen Region I' und I.
Jeder Punkt im Kruskal-Diagramm stellt eine Kugel mit der
Fläche 4\pi r^2 dar. Im Koordinatenursprung selbst ist r=2m, die
Fläche der Kugel somit 16\pi m^2; der Schnitt entlang dieser
Koordinatenlinie wird als die Einstein-Rosen-Brücke bezeichnet, als
`Tor zu einem anderen Universum'. Dieses andere Universum kann jedoch
nie betreten werden, nur ein Beobachter innerhalb des Schwarzschildradius
kann dessen Existenz bemerken (Vgl. Hawking, pp. 149).
Die Koordinatenlinien konstanter Schwarzschildzeit in der Außenregion I
treten dabei in der unsichtbaren zweiten Außenregion I' in
umgekehrter Reihenfolge auf, dort scheint die Zeit von
t=+\infty nach t=-\infty zu laufen
(scheinbar, da die Koordinate t auf
die Eigenschaften der Region I hin gemünzt wurde).
Die mithilfe der Kruskal-Szekeres-Koordinaten durchgeführte Erweiterung
der Schwarzschildlösung ist maximal, da alle Geodäten entweder
bis zu einem beliebig großen Bahnparameter ausgedehnt werden können oder
bei einem endlichen Wert die Singularität bei r=0 erreichen.
Um auch Punkte, die im Unendlichen liegen, in einer Karte darstellen zu
können, ist es nützlich, eine neue Koordinatentransformation
\bar{\bar x}=\mtext{arctan}(\bar x) und
\bar{\bar t}=\mtext{arctan}(\bar t) einzuführen.
Punkte bei +\infty(-\infty) werden so
auf +\pi/2(-\pi/2) abgebildet;
diese Darstellung wird als Penrose-Diagramm bezeichnet.
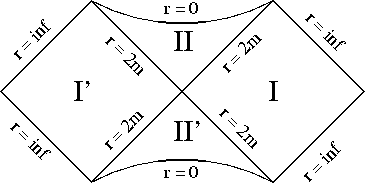
Penrose-Diagramm
4.10 Darstellung in der Schwarzschild-Karte